I. INTRODUCTION

Temperature sensors used in harsh environments, such as geothermal power plants ^[1] and automotive applications ^[2], should operate reliably over an extended temperature range, reaching up to $+150^\circ$C, exceeding the military temperature range of $+125^\circ$C commonly supported by typical temperature sensors ^[3,4]. In such high-temperature environments, discrete sensors like thermistors and platinum resistors have traditionally been preferred due to their reliable resistance-temperature (R/T) characteristics and consistent performance ^[5]. Despite these advantages, discrete sensors have limitations, such as size, power consumption, and interoperability issues with other electronic devices. CMOS integrated temperature sensors, using MOSFETs, resistors, or BJTs, enable the integration of temperature sensing, digital value conversion, and interfacing on a single chip, which helps to mitigate the limitations of discrete sensors ^[6,7,8,9,10]. Even so, MOSFET-based and resistor-based sensors suffer from high sensitivity to process variations and often require two-point trimming to achieve acceptable accuracy which increases production costs ^[9,11]. In contrast, BJT-based sensors utilize the predictable temperature dependence of the base-emitter voltages (${V}_{\rm BE}$s) to offer a wide temperature range with high accuracy and reduced sensitivity to process variations, requiring only one-point trimming ^[12,13]. However, at high temperatures, the leakage current of CMOS components increases significantly, which can lead to temperature sensing errors and impose limitations on the operating range of temperature sensors ^[12].

This paper proposes a BJT-based CMOS temperature sensor that achieves an inaccuracy of $\pm0.94^\circ$C ($3 \sigma$) after one-point trimming over an extended temperature range from $-40^\circ$C to $+150^\circ$C. To enhance the accuracy of temperature sensing, $\beta$-compensation technique and bitstream-controlled dynamic element matching (DEM) are applied to the sensing frontend. To reduce the number of required sampling switches, only two sampling capacitors are employed in the first integrator of the readout circuit ^[13]. This design choice alleviates the impact of sampling switch leakage currents, which worsen at high temperatures.

The rest of this paper is organized as follows: Section II explains the operating principle of the temperature sensor. The implementation of the proposed sensor is described in Section III. Section IV presents the measurement results and Section V concludes this paper.

II. OPERATING PRINCIPLE OF BJT-BASED TEMPERATURE SENSOR

Fig. 1 illustrates the basic operation of a temperature sensor utilizing PNP transistors. The $Q_{0}$ and $Q_{1}$ produce $V_{\rm BE}$${}_{0}$ and $V_{\rm BE1}$, respectively, which exhibit complementary-to-absolute-temperature (CTAT) ^[14], that can be expressed as

where ${k}$ is Boltzmann's constant, ${T}$ is the absolute temperature, ${q}$ is the electron charge, ${I}_{\rm S}$ is the transistor's saturation current, $\beta$ is the forward current gain, ${I}_{\rm BIAS}$ is bias current of PNP transistor, and $p$ is bias current ratio. The resulting voltage difference between the two PNP transistors is proportional-to-absolute-temperature (PTAT) ^[14], given by

with an assumption of sufficiently large values of $\beta$. In Eq. (3), if ${I}_{\rm BIAS} \gg I_{\rm S}$, $\Delta {V}_{\rm BE}$ exhibits linear behavior with respect to temperature ^[12]. Additionally, it indicates that $\Delta V_{\rm BE}$ only depends on the current ratio ${p}$, making it insensitive to process spread. Fig. 2 shows the temperature dependency of voltages for temperature sensing. The temperature-independent ${V}_{\rm REF}$ is obtained by adding ${V}_{\rm BE1}$ and $\alpha \cdot \Delta V_{\rm BE}$, where $\alpha$ is the gain coefficient ^[3]. The readout circuit digitizes the ratio of $\alpha \cdot \Delta V _{\rm BE}$ and ${V}_{\rm REF}$ to obtain PTAT output $\mu$, as shown below:

This PTAT output is converted to a Celsius value through scaling with batch calibration, as follows:

where ${D}_{out}$ is Celsius value of sensed temperature, and ${A}$ and ${B}$ are calibration parameters. This readout method ^[3] is not flexible because it digitizes $\mu$ using the coefficient $\alpha$ fixed on-chip. In contrast, as shown in Fig. 3, this paper employs a readout method using gain coefficient $\alpha$* determined off-chip through batch calibration for flexibility ^[10]. To apply this method, the readout circuit digitizes the ratio $Y = {k}\cdot \Delta V_{\rm BE} / V_{\rm BE1}$ instead of directly digitizing the $\mu$, where $\Delta V_{\rm BE}$ serves as the input signal, ${V}_{\rm BE1}$ as the reference signal, and ${k}$ is a gain factor. As shown in Fig.~4, the gain factor ${k}$ is applied to enhance the utilization of the dynamic range ^[4]. In this paper, ${k}$ is implemented as 4 using a switched-capacitor circuit, considering both the dynamic range and design complexity. Although this ratio $Y$ is not linear with respect to temperature, the linear PTAT output $\mu ^{*}$ can be obtained off-chip using the $Y$ ^[13] and is given by

where $\alpha^*$ is the batch calibration parameter.

Fig. 1. Basic operation of a PNP transistor-based temperature sensor.

Fig. 2. Temperature dependency of voltages for temperature sensing.

Fig. 3. Readout method of the proposed temperature sensor using off-chip gain coefficient.

Fig. 4. Simulation results of digitized ratio w/ and w/o gain factor.

III. IMPLEMENTATION

As shown in Fig. 5, the proposed temperature sensor consists of three main parts: a sensing frontend, a readout circuit, and a digital controller. The sensing frontend employs BJTs to generate ${V}_{\rm BE0}$ and ${V}_{\rm BE1}$. These signals are

processed by the readout circuit, utilizing the 1-bit second-order incremental delta-sigma analog-to-digital converter ($\Delta \Sigma$ ADC) to produce digital values for temperature reading. The digital controller provides control signals and clocks required for overall operation.

To achieve the accuracy requirements of the temperature sensor with only a single PTAT trimming at room temperature (RT), error sources that contribute to non-PTAT errors should be mitigated ^[3]. Therefore, errors caused by device mismatches and finite $\beta$ should be mitigated to make the PTAT error due to process spread in ${V}_{\rm BE}$ the dominant error source ^[15].

Fig. 5. Block diagram of the proposed temperature sensor.

1. Sensing Frontend

1) Circuit overview: Fig. 6 shows the circuit diagram of the sensing frontend, which consists of the biasing circuit and the bipolar core. The PTAT bias current is generated by the feedback loop which includes an error amplifier, current sources, polysilicon resistors, and PNP transistors. The biasing circuit forces the difference between $V_{\rm BE}$s ($\Delta$$V_{\rm BE}$) of the $Q_{\rm BIAS0}$ and $Q_{\rm BIAS1}$ across the resistors ($R_{\rm BIAS0}$ or $R_{\rm BIAS1}$) to generate a PTAT I${}_{\rm BIAS}$. The generated current is mirrored through the current sources to bias $Q_{0}$ and $Q_{1}$, generating $V_{\rm BE0}$ and $V_{\rm BE1}$ in the bipolar core ^[3].

2) Error reduction design techniques: If $\beta$ is sufficiently large such that $\beta /(\beta+1)$ effectively equals 1, the influence of $\beta$ spread in Eqs. (1) and (2) can be neglected. However, in the process used, the $\beta$ of the PNP transistor is approximately 3.5, causing $V_{\rm BE}$ to exhibit a non-PTAT error resulting from the $\beta$ spread ^[16]. Therefore, a $\beta$-compensation technique is employed to generate the $I_{\rm BIAS}$ proportional to $(\beta+1)/\beta$ ^[16]. Assume that the $\beta$ of all four PNP transistors are the same. The $I_{\rm BIAS}$ with the $\beta$-compensation technique can be expressed as

(7)

$ I_{\mathrm{BIAS}}=\frac{\Delta V_{\mathrm{BIAS}}}{R_{\mathrm{BIAS}}} \cdot \frac{\beta +1}{\beta }. $

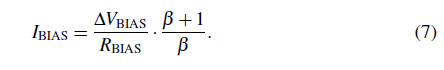
Substituting $I_{\rm BIAS}$ from Eqs. (7) into (1) and (2) yields

(8)

$V_{\mathrm{BE0}}=\frac{kT}{q}\ln \left(\frac{\Delta V_{\mathrm{BIAS}}}{R_{\mathrm{BIAS}}} \cdot \frac{\beta +1}{\beta } \cdot \frac{1}{I_{\mathrm{S}}} \cdot \frac{\beta }{\beta +1}+1\right)$

$ \hskip 1.5pc =\frac{kT}{q}\ln \left(\frac{\Delta V_{\mathrm{BIAS}}}{R_{\mathrm{BIAS}}} \cdot \frac{1}{I_{\mathrm{S}}} +1\right), $

(9)

$V_{\mathrm{BE1}}=\frac{kT}{q}\ln \left(\frac{\Delta V_{\mathrm{BIAS}}}{R_{\mathrm{BIAS}}} \cdot \frac{\beta +1}{\beta } \cdot \frac{p}{I_{\mathrm{S}}} \cdot \frac{\beta }{\beta +1}+1\right)$

$ \hskip 1.5pc = \frac{kT}{q}\ln \left(\frac{\Delta V_{\mathrm{BIAS}}}{R_{\mathrm{BIAS}}} \cdot \frac{p}{I_{\mathrm{S}}}\ +1\right). $

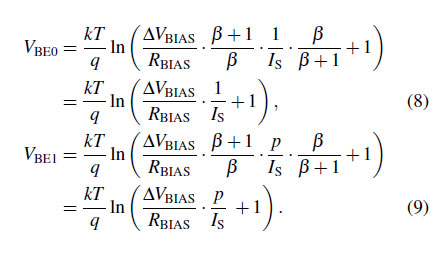
This technique makes the $V_{\rm BE}$s of the $Q_{0}$ and $Q_{1}$ independent of $\beta$ by canceling out $\beta/(\beta+1)$ in Eqs. (1) and (2). The accuracy of the $\beta$-compensation technique can be degraded by the $\beta$ mismatch of the four PNP transistors ($Q_{\rm BIAS0}$, $Q_{\rm BIAS1}$, $Q_{0}$, and $Q_{1}$) ^[17]. To mitigate the mismatch of the $\beta$ without quantization noise folding, bitstream-controlled DEM is employed ^[11,15]. However, at high temperatures, $I_{\rm S}$, which is proportional to the emitter area, increases exponentially with temperature ^[12], resulting in significant nonlinearity in both $V_{\rm BE}$ and $\Delta$$V_{\rm BE}$ ^[10]. Therefore, the PNP transistors in the sensing frontend are designed with consideration for matching requirements and the impact of $I_{\rm S}$ at high temperatures.

3) Implementation: The biasing circuit and the bipolar core each use a pair of 2 $\mu$m $\times$ 2 $\mu$m PNP transistors: $Q_{\rm BIAS0}$ and $Q_{\rm BIAS1}$, and $Q_{0}$ and $Q_{1}$, respectively. Total 12 unit current sources are employed to bias the $Q_{\rm BIAS0}$, $Q_{\rm BIAS1}$ pair and the $Q_{0}$, $Q_{1}$ pair at the 1:5 ratio with DEM switches to average the unit bias current $I_{\rm BIAS}$. The $I_{\rm BIAS}$ value is set to 300 nA (at $27^\circ$C) with $R_{\rm BIAS0} = R_{\rm BIAS1} = 175$ k$\Omega$, considering the power consumption and the settling requirement of the sampling capacitor in the readout circuit. A conventional folded-cascode topology with a dc gain of over 84 dB across the operating temperature range is used for the error amplifier ${A}_{\rm E}$ in the biasing circuit. As the offset and $1/{f}$ noise of the ${A}_{\rm E}$ cause non-PTAT errors, chopping is employed to mitigate them ^[11].

$\beta$-compensation technique is implemented by adding resistors ${R}_{\beta0}$ ($= R_{\rm BIAS0}/5$) and ${R}_{\beta1}$ ($= R_{\rm BIAS1}/5$) in series with the bases of $Q_{\rm BIAS0}$ and $Q_{\rm BIAS1}$ in the biasing circuit, respectively. To enable swapping between $Q_{\rm BIAS0}$ and $Q_{\rm BIAS1}$ in the biasing circuit, the $R_{\rm BIAS0}$, ${\mathrm{R}}_{\beta0}$ pair and the $R_{\rm BIAS1}$, ${R}_{\beta1}$ pair are connected, respectively. Similarly, in the bipolar core, DEM logic swaps $Q_{0}$ and $Q_{1}$ by exchanging the current ratio.

Fig. 6. Circuit diagram of the sensing frontend.

2. Readout Circuit

1) Architecture: At high temperatures, the leakage current of the sampling switches increases. Fig. 7 shows the simplified sampling network and associated leakage paths. $I_{leak1}$ is caused by reverse diodes in the on-state switch, while $I_{leak2}$ and $I_{leak3}$ are due to the off resistance of the off-state switches ^[13]. These leakages not only distort the bias current in the bipolar core transistors but also introduce errors in the charge sampled onto the sampling capacitors. Since both on-state and off-state switches induce leakage paths, these effects are proportional to the total number of switches in the sampling network ^[12,13]. Unlike the two architectures presented in ^[3] and ^[18], this paper employs a readout circuit with only two differential sampling capacitors, as in ^[13]. This approach significantly reduces the total number of required switches to six, compared to the zoom ADC architecture in ^[18], which relies on hundreds of sampling and DEM switches. Consequently, both the reduced number of sampling switches and the absence of DEM switches in the capacitor array mitigate the impact of switch leakage currents in the sampling network at high temperatures.

A required ADC resolution to achieve a temperature sensing resolution of less than $0.025^\circ$C can be calculated by the following equation ^[10]:

(10)

$ \text{Required ADC resoltuion}= \log_2 \left(\frac{{\partial {\mu }^*}/{\partial Y}}{{\partial {\mu }^*}/{\partial T}}\cdot \frac{1}{S}\right), $

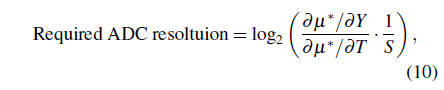
where the ${S}$ is target sensing resolution, $Y$ ($= 4 \cdot \Delta V_{\rm BE}/V_{\rm BE1}$) is the digitized ratio, and $\mu^{*}$ is the linear PTAT output. Based on the simulation results, the required ADC resolution is determined to be 15.5-bit.

2) Charge-Balancing: Figs. 8 and 9 illustrate a circuit diagram of the readout circuit and its simplified timing diagram. Detailed charge-balancing process for digitizing the ${Y} = 4 \cdot \Delta V_{\rm BE}/V_{\rm BE1}$ is as follows: At each $\Phi_{\Delta \Sigma }$ period, the first integrator samples either $V_{\rm BE0}$ or $\Delta V_{\rm BE}$ during four clock phases $\Phi_{1}$ and $\Phi_{2}$, with the total sampled charge varying depending on the ${bs}$. When ${bs} = 0$, $\Delta V_{\rm BE}$ is sampled four times, integrating a charge proportional to $4 \cdot \Delta V_{\rm BE}$. While, when ${bs} = 1$, $\Delta V_{\rm BE}$ is sampled three times and $- V_{\rm BE0}$ is sampled once, resulting in a charge proportional to $3 \cdot \Delta V_{\rm BE} - V_{\rm BE0}$. Due to the ADC's feedback, the average integrated charge is zero, and with the average of ${bs}$ defined as $Y$, this charge-balancing scheme satisfies the following equation ^[3]:

(11)

$ (1-Y)\cdot (4\cdot \Delta V_{\mathrm{BE}})+Y\cdot (3\cdot \Delta V_{\mathrm{BE}}-V_{\mathrm{BE0}})=0. $

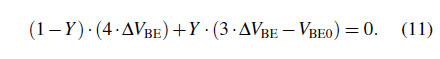
As $3 \cdot \Delta V_{\rm BE} - V_{\rm BE0}$ is equivalent to $4 \cdot \Delta V_{\rm BE} - V_{\rm BE1}$, Eq. (11) can be calculated as shown in the following equations ^[19]:

(12)

$ (1-Y)\cdot (4\cdot \Delta V_{\mathrm{BE}})+Y\cdot (4\cdot \Delta V_{\mathrm{BE}}-V_{\mathrm{BE1}})=0, $

(13)

$ Y=\frac{4\cdot \Delta V_{\mathrm{BE}}}{V_{\mathrm{BE1}}}. $

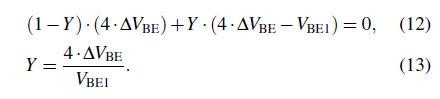
As a result, through Eqs. (11) to (13), this scheme generates the previously mentioned ratio $Y$.

3) Implementation: The circuit diagram of the readout circuit is illustrated in Fig. 8. Only two differential sampling capacitors are employed to sample $V_{\rm BE0}$, $V_{\rm BE1}$, and gnd using six sampling switches. Additionally, to reduce leakage current in the off-state, the switches connected to gnd are implemented using high-threshold voltage devices. The size of the C${}_{S1}$ is set to 2.5 pF, considering the ${kT}/{C}$ noise, while C${}_{S2}$, C${}_{A}$, and C${}_{FF}$ are set to 200 fF, given the relaxed conditions due to noise shaping ^[16,20]. $A_{1}$ and $A_{2}$ employ folded-cascode OTAs, providing a dc gain of over 97 dB across the operating temperature range. Correlated-double sampling is used to reduce offset and $1/{f}$ noise of the first integrator ^[21]. System-level low-frequency chopping (CHL) is further applied to address residual offset ^[19]. The CHL is implemented digitally, eliminating the need for additional switches.

Simplified timing diagram is shown in Fig. 9. The first integrator operates with non-overlapping clocks, $\Phi_{1}$ and $\Phi_{2}$, while the second integrator and the switched capacitor adder operate at half the frequency of the first integrator, using duty-cycle-adjusted non-overlapping clocks, $\Phi_{3}$ and $\Phi_{4}$. The first integrator samples outputs of the sensing frontend ($V_{\rm BE0}$ and $V_{\rm BE1}$) or gnd during four clock phases $\Phi_{1}$ and $\Phi_{2}$, based on the value of ${bs}$. During the fourth phase, the first integrator's output is sampled onto $C_{\rm S2}$ of the second integrator during $\Phi_{4}$ phase and subsequently integrated during the following $\Phi_{3}$ phase. The ${bs}$ is generated by the single-bit quantizer with $\Phi_{\Delta \Sigma}$. Oversampling ratio (OSR) of 512 is employed to achieve the required ADC resolution ^[22].

Fig. 7. Simplified sampling network and associated leakage paths.

Fig. 8. Circuit diagram of the readout circuit.

Fig. 9. Timing diagram of the readout circuit.

IV. MEASUREMENT RESULTS

The temperature sensor is implemented in a 0.18-$\mu$m CMOS process. The die micrograph is shown in Fig. 10 with an area of 0.63 mm${}^{2}$. The sinc${}^{2}$ decimation filter and the batch calibration were implemented off-chip for flexibility. This sensor draws 12.35 $\mu$A from a 1.8 V supply with a conversion time of 20 ms. At $27^\circ$C, 100 consecutive temperature readings are taken to measure the resolution, as shown in Fig. 11. This sensor achieves a resolution of 6.9 mK under 20 ms conversion time at RT, resulting in a resolution figure of merit (FoM) of 21.17 pJ$\cdot$K${}^{2}$.

To measure the inaccuracy of the temperature sensor, six samples are tested across the temperature range from $-40^\circ$C to $+150^\circ$C in the temperature chamber. One-point trimming is implemented off-chip by applying a trimming coefficient $\Delta \alpha$, which sets the temperature error to zero at the trimming temperature (RT), as shown in the following equation ^[19]:

Fig. 12 shows the measured inaccuracy without applying bitstream-controlled DEM after batch calibration. The sensor exhibits an inaccuracy of ${\pm} 4.44 ^\circ$C ($3 \sigma$) before trimming, which is reduced to ${\pm} 4.30 ^\circ $C ($3 \sigma$) after one-point trimming. The absence of bitstream-controlled DEM substantially increases the temperature error over the operating temperature range, due to the mismatch among the PNP transistors and current sources. Moreover, since this temperature error is not the PTAT error, it cannot be effectively compensated by one-point trimming ^[3]. With bitstream-controlled DEM, the measured inaccuracy of the proposed temperature sensor is improved to $\pm 1.14^\circ$C ($3 \sigma$) before trimming and $\pm 0.94^\circ$C ($3 \sigma$) after one-point trimming as shown in Fig. 13. Table 1 provides a summary of the measured performance of this temperature sensor and a comparison with other temperature sensors.

Fig. 10. Die micrograph.

Fig. 11. Measured temperature resolution at $27^\circ$C.

Fig. 12. Measured inaccuracy without applying bitstream-controlled DEM (a) before trimming and (b) after one-point trimming.

Fig. 13. Measured inaccuracy with applying bitstream-controlled DEM (a) before trimming and (b) after one-point trimming.

Table 1. Performance summary and comparison table.

V. CONCLUSIONS

This paper presents a BJT-based CMOS temperature sensor with an extended temperature range from $-40 ^\circ$C to $+150^\circ$C. To reduce the non-PTAT error caused by mismatch of $\beta$ and current sources in the sensing frontend, $\beta$-compensation and bitstream-controlled DEM are employed. In the readout circuit, only two sampling capacitors and digital CHL are implemented to reduce the number of switches, mitigating the impact of switch leakage current at high temperatures. Fabricated in a 0.18-$\mu$m CMOS process, the proposed sensor occupies an area of 0.63 mm$^2$ and consumes 22.23 $\mu$W from a 1.8 V supply at 27$^\circ$C. It achieves a resolution FoM of 21.17 pJ$\cdot$K${}^{2}$ and an inaccuracy of $\pm 0.94^\circ$C ($3 \sigma$) after one-point trimming, with a conversion time of 20 ms.